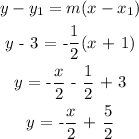ANSWER
The equation of the line tangent to the function at the given point is:
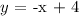
Explanation
The given equation is:

Step 1: Determine the 1st derivative of the equation
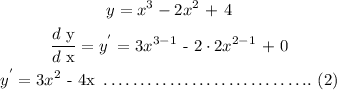
Step 2: To determine the slope (m) of the tangent line, insert the x-value (1) into the equation 2
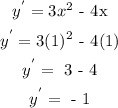
Step 3: use the point-slope formula to determine the equation of the line tangent to the given function at x = 1
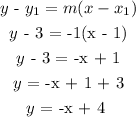
Hence, The equation of the line tangent to the function at the given point is:
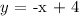
=======================================================================
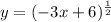
1. Take 1st derivative
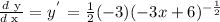
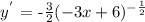
2. insert the x-value (-1) to determine the slope (m)
![\begin{gathered} y^{^(\prime)}\text{ = -}(3)/(2)(-3(-1)+6)^{-(1)/(2)} \\ y^{^(\prime)}\text{ = -}(3)/(2)(9)^{-(1)/(2)} \\ y^{^(\prime)}\text{ = -}(3)/(2)(\frac{1}{\sqrt[]{9}}) \\ y^{^(\prime)}\text{ = -}(3)/(2)\text{ }\cdot\text{ }(1)/(3) \\ y^{^(\prime)}\text{ = -}(1)/(2) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/88r9tfoufobq8ga0fiy0310sln0n12u6fn.png)
3. Now, determine the equation of the line tangent at (-1,3)