Explanation
We are asked to find the interest rate that will yield $1500 for a sum of $1000 invested quarterly

In our case, we have
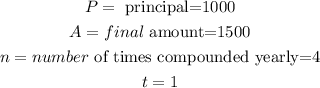
Thus, we will have
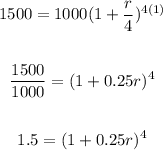
Solving for r
we will have
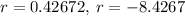
Since the value increased, the rate will be positive
Therefore
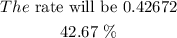
To the nearest per cent, we will have the annual rate as 42.7 %