The rational function will have the next form:
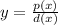
where p(x) and d(x) are two polynomials.
Given that the function has a vertical asymptote at x = 2, then d(x) must have a zero at x = 2. Since this is the only asymptote, then:
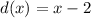
A slant asymptote is present when the degree of the polynomial of the numerator is exactly one more than the degree of the denominator. This means that p(x) must be a polynomial a degree 2.
The quotient, q(x), between p(x) and d(x) is the equation of the slant asymptote. The next relation must be satisfied:
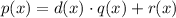
where r(x) is the remainder of the division. Assuming the remainder is a constant, k, and substituting with d(x) = x-2 and q(x) = x + 2, the slant asymptote, we get:
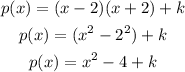
We know that the curve passes through the point (3, 8), that is, when x = 3, then y = 8. Substituting with this point and the functions p(x) and d(x), we get:
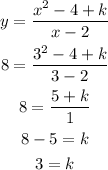
Finally, the rational function is:
