Question

Write a recursive formula for the sequence 6, 9, 13.5, 20.25, ….. Can someone please help me with this I have no idea how to do this!

Answer 1

We have to write a recursive formula for the sequence 6, 9, 13.5, 20.25...

A recursive formula is a formula where the term value depends on the previous term value:

`a_n=f(a_(n-1))`

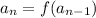
In this case, as there is no common difference, we can conclude that this is not a arithmetic sequence.

We will test if we have a common ratio between the terms:

`\begin{gathered} (a_2)/(a_1)=(9)/(6)=1.5 \\ (a_3)/(a_2)=(13.5)/(9)=1.5 \\ (a_4)/(a_3)=(20.25)/(13.5)=1.5 \end{gathered}`

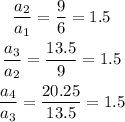
We have a common ratio between consecutive terms and its value is r=1.5.

Then we have a geometric sequence and we can write the recursive formula as:

`\begin{gathered} a_n=r\cdot a_(n-1) \\ a_n=1.5\cdot a_(n-1) \end{gathered}`

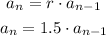
You can find new terms multiplying the previous term value by 1.5.

Answer: the recursive formula is a(n) = 1.5 * a(n-1)