We have to write a recursive formula for the sequence 6, 9, 13.5, 20.25...
A recursive formula is a formula where the term value depends on the previous term value:

In this case, as there is no common difference, we can conclude that this is not a arithmetic sequence.
We will test if we have a common ratio between the terms:
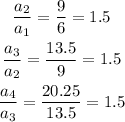
We have a common ratio between consecutive terms and its value is r=1.5.
Then we have a geometric sequence and we can write the recursive formula as:
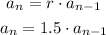
You can find new terms multiplying the previous term value by 1.5.
Answer: the recursive formula is a(n) = 1.5 * a(n-1)