ANSWER
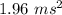
Step-by-step explanation
We want to find the resulting acceleration of the object.
To do this, we apply the formula for the net force acting on the object:
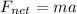
where Fnet = net/total force acting on the object
m = mass
a = acceleration
The net force is the sum of the applied force and the frictional force (which is negative):
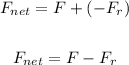
Substitute that into the equation for net force and solve for a:
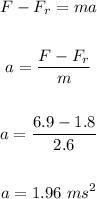
That is the acceleration.