Given
A = (3k,8)
B = (k, -3)
Gradient AB = 3
And we have that the gradient of a line joining the two points A and B is:
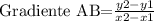
Therefore, we substitute the given values into the gradient equation:
Gradient AB = 3
x1 = 3k
y1 = 8
x2 = k
y2 = -3
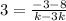
Then, solve for k.
Simplify:
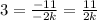
Multiply by 2k on both sides:
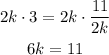
Divide by 6 on both sides:

Answer: k = 11/6