Question

Jeremy needs to cut a triangular piece of tile for a mosaic. In order to cut it properly, he needs to know the measure of the angle marked as shown in the figure. The lengths of XY, Y Z, and XZ are 110 millimeters, 141 millimeters, and 203 millimeters respectively. What is the value of ?? (Round your answer to the nearest degree if necessary. Do not include any units.)

Answer 1

From the given triangle, the dimensions are

To find the unknown angle, we find angle m∠Y

Using the cosine rule formula which is shown below

`\cos Y=(x^2+z^2-y^2)/(2xz)`

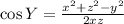
Where

`\begin{gathered} XY=z \\ YZ=x\text{ and} \\ XZ=y \end{gathered}`

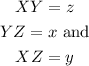
Substitute the values of x, y and z into the cosine rule formula

`\begin{gathered} \cos Y=(x^2+z^2-y^2)/(2xz) \\ \cos Y=(141^2+110^2-203^2)/(2(141)(110)) \\ \cos Y=(-9228)/(31020)=-0.2975 \\ Y=\cos ^(-1)(-0.2975) \\ Y=107.3^0 \end{gathered}`

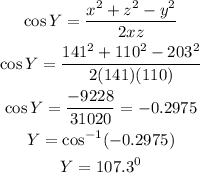
Let the unknown angle be k, since m∠Y is known,

`k+m\angle Y=180^0\text{ (angle on a straight line)}`

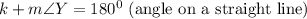
Substitute 107.3° of m∠Y into the formula above

`\begin{gathered} k+m\angle Y=180^0 \\ k+107.3^o=180^o_{} \\ \text{Collect like terms} \\ k=180^o-107.3^{} \\ k=72.7^0 \\ k=73^o\text{ (nearest degree)} \end{gathered}`

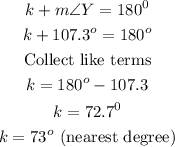
Hence, the unknown angle 73^