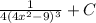Given the integral function below
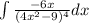
a) The inside function is
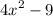
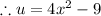
The derivative of the inside function is
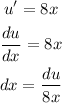
b) Therefore, the integral can be written as:
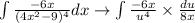
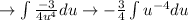


Final answer:
a) The inside function is 4x² - 9, and the derivative is 8x
b) The integration by substitution is