We are given a table of values of a line function.
The y-intercept of a line is the point where the line intercepts the y-axis. At this point, the value of "x" is zero.
From the table, we look in the row for the x-values the entry for zero. The associated value to that entry is the y-intercept, therefore, we have:

To determine the slope we will use the following formula:

Where:
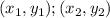
are values in the table. We choose the first two values:
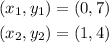
Substituting the values we get:
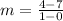
Solving the operations:
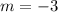
Therefore, the slope is -3
To determine the equation of the line we use the slope-intercept form of a line equation:

Where "m" is the slope, and "b" is the y-intercept.
Substituting we get:
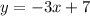
And thus we get the equation of the line.