Question

A table of values of a linear function is shown below

Answer 1

We are given a table of values of a line function.

The y-intercept of a line is the point where the line intercepts the y-axis. At this point, the value of "x" is zero.

From the table, we look in the row for the x-values the entry for zero. The associated value to that entry is the y-intercept, therefore, we have:

`y-intercept=7`

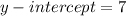
To determine the slope we will use the following formula:

`m=(y_2-y_1)/(x_2-x_1)`

Where:

`\begin{gathered} (x_1,y_1);(x_2,y_2) \\ \end{gathered}`

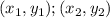
are values in the table. We choose the first two values:

`\begin{gathered} (x_1,y_1)=(0,7) \\ (x_2,y_2)=(1,4) \end{gathered}`

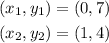
Substituting the values we get:

`m=(4-7)/(1-0)`

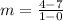
Solving the operations:

`m=-3`

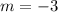
Therefore, the slope is -3

To determine the equation of the line we use the slope-intercept form of a line equation:

`y=mx+b`

Where "m" is the slope, and "b" is the y-intercept.

Substituting we get:

`y=-3x+7`

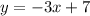
And thus we get the equation of the line.