Question

What is the value of x ?x=(simplify your answer . Type an exact answer , using radicals as needed. )

Answer 1

Step1:

The triangle under considration is a right angle triangle

Step 2:

One of the required trigonometric ratios that is helpful here is;

`\begin{gathered} \sin \text{ }\theta\text{ = }\frac{\text{opposite}}{\text{hypotenuse}} \\ \\ \sin \text{ 45 = }(13)/(x) \end{gathered}`

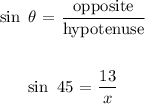
Step 3:

Crossing multiplication;

x sin 45 = 13

Step 4:

Dividing both sides by sin 45

`\begin{gathered} x\text{ = }\frac{13}{\sin \text{ 45}} \\ x=13\text{ / }\frac{1}{\sqrt[]{2}} \\ x\text{ = 13 x }\frac{\sqrt[]{2}}{1} \\ x\text{ = 13 }\sqrt[]{2} \end{gathered}`

Conclusion:

The value of x in the figure given is 13 root 2