Question

Write two polynomial functions whose quotients will have a degree of zero.

Answer 1

`\begin{gathered} f(x)=6x^2+4x+2 \\ g(x_{})=18x^2+12x+6 \end{gathered}`

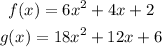
Step-by-step explanation:

Definition:

The degree of a polynomial is the highest index/power of the variable in the polynomial.

The quotient of two polynomials will have a degree of zero if they are multiples of one another.

Let the two polynomial functions be:

`\begin{gathered} f(x)=6x^2+4x+2 \\ g(x_{})=18x^2+12x+6 \end{gathered}`

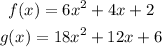
Its quotient:

`\begin{gathered} (f(x))/(g(x))=(6x^2+4x+2)/(18x^2+12x+6) \\ =(2(3x^2+2x+1))/(6(3x^2+2x+1)) \\ =(2)/(6) \\ =(1)/(3) \end{gathered}`

Note:

`(1)/(3)=(1)/(3)x^0`

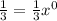
Since the quotient is a constant, it has a degree of zero.