Question

sweredAnsweredQuestion 1rrect Answer0/1 ptsA chunk of material has a mass of 328. g and a specific heatof 1.17 J/g °C. Suppose its initial temperature is 71.0 °C.Calculate the final temperature of the chunk after it loses 8.7kJ of heat in a pot of water. Enter your answer to 1 decimalplace.48.3 margin of error +/- 0.2

Answer 1

48.3 °C

Step-by-step explanation

Given parameters:

Mass of the chunk material, m = 328.0 g

The specific heat of the material, c = 1.17 J/g°C

Initial temperature, T₁ = 71.0 °C

The heat lost, Q = 8.7 kJ = 8700 J

What to find:

The final temperature (T₂) of the chunk after it loses 8.7 kJ of heat in a pot of water.

Step-by-step solution:

The final temperature (T₂) of the chunk after it loses 8.7 kJ of heat in a pot of water can be calculated using the formula for heat lost.

`-Q=mc(T_2-T_1)`

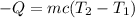
Putting the values of the given parameters into the formula, we have:

`\begin{gathered} -8700\text{ }J=328.0\text{ }g*1.17\text{ }J\text{/}g°C*(T_2-71.0°C) \\ \\ -8700\text{ }J=383.76\text{ }J\text{/}°C*(T_2-71.0°C) \\ \\ -8700\text{ }J=(383.76J\text{/}°C* T_2)-(383.76J\text{/}°C*71.0°C) \\ \\ -8700\text{ }J=(383.76\text{ }J\text{/}°C* T_2)-27246.96J \\ \\ 383.76\text{ }J\text{/}°C* T_2=-8700J+27246.96J \\ \\ 383.76\text{ }J\text{/}°C* T_2=18546.96J \\ \\ Divide\text{ }both\text{ }sides\text{ }by\text{ }383.76\text{ }J\text{/}°C \\ \\ \frac{383.76\text{ }J\text{/}°C* T_2}{383.76\text{ }J\text{/}°C}=\frac{18546.96J}{383.76\text{ }J\text{/}°C} \\ \\ T_2=48.3°C \end{gathered}`

Therefore, the final temperature of the chunk after it loses 8.7 kJ of heat in a pot of water is 48.3 °C.