Question

Find the vertical asymptote of the graph of the function.f(x)= 1 —————- (x-2)^2 The equation of the vertical asymptote isX=

Answer 1

Answer:

The eqaution is given below as

`f(x)=(1)/((x-2)^2)`

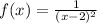
Concept:

A vertical asymptote is a vertical line that guides the graph of the function but is not part of it. It can never be crossed by the graph because it occurs at the x-value that is not in the domain of the function.

To do this, we will have to look for the value of x that makes the equation undefined.

That is, we will susbtitute the denominator=0

By applying the concept,we will have

`\begin{gathered} (x-2)^2=0 \\ sqare\text{ root both sides, we will have} \\ x-2=0 \\ add\text{ 2 to both sides,we will have} \\ x-2+2=0+2 \\ x=2 \end{gathered}`

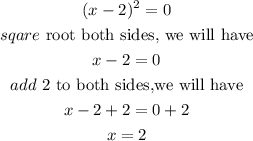
Representing graphically, we will have the vertical symptotes to be

Hence,

The equation of the vertical asymptote is

`x=2`