1 Answer

Henriale · Answer 1 · 2023-04-11T15:41:46+0000

we have the inequality

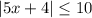
$\lvert5x+4\rvert\leq10$

step 1

Find out the first solution (positive case)

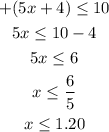
$\begin{gathered} +(5x+4)\leq10 \\ 5x\leq10-4 \\ 5x\leq6 \\ x\leq(6)/(5) \\ x\leq1.20 \end{gathered}$

The first solution is all real numbers less than or equal to 1.20

Interval (-infinite,1.20]

step 2

Find out the second solution (negative case)

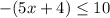
$-(5x+4)\leq10$

Multiply by -1 both sides

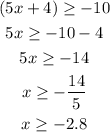
$\begin{gathered} (5x+4)\ge-10 \\ 5x\ge-10-4 \\ 5x\ge-14 \\ x\ge-(14)/(5) \\ x\ge-2.8 \end{gathered}$

The second solution is all real numbers greater than or equal to -2.8

the interval [-2.8, infinite)

step 3

Find out the solution to the given inequality

The solution is

[-2.8, infinite) ∩ (-infinite,1.20]=[-2.8,1.20]

the solution is the interval [-2.8,1.20]

see the attached figure to better understand the problem

Please log in or register to add a comment.