Since we need to choose groups of 6 from 17 options, we call this "17 choose 6". This is the same as the nCr formula for "n choose r", so we need to use:
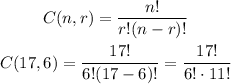
Since factorial is the multiplication of the factors from the given one to 1, 17! divided by 11! cancels out all the factors from 11 to 1 of the 17!, so we are left with:
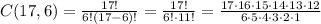
Now, we can cancel some factors out before evaluating everthing:
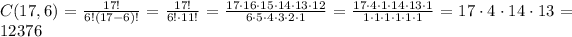
So, the number of combinations is 12376.