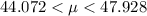Step 1: Find the t-value

The intersection is 2.101, which means that our t-value is 2.101.
Step 2: Calculate the standard error
![\begin{gathered} \text{SE}=\frac{s}{\sqrt[]{n}}=\frac{4}{\sqrt[]{19}} \\ \text{SE}=0.9176629355 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/26mjq3cpq7cz9n72zkwyabbanjyjwrhbi8.png)
Step 3: Multiply the t-value to the standard error
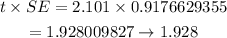
Step 4: Add and Subtract it to the sample mean, to get the lower and upper limit.

Final Step: Now that we have Upper and Lower limit, our confidence interval is: