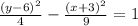Question

Find an equation of the hyperbola having foci at (-3, 3) and (-3,9) and vertices at (-3, 4) and (-3,8).

Answer 1

Given:

Foci of the hyperbola = (-3,3), (-3, 9)

Vertices of the hyperbola = (-3, 4), (-3, 8)

Required: Equation of the hyperbola

Step-by-step explanation:

The x-coordinates of the vertices and foci are same, so the transverse axis is parallel to the y-axis. Thus, the equation of the hyperbola will have the form

`((y-k)^2)/(a^2)-((x-h)^2)/(b^2)=1`

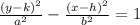
First, identify the center (h, k). The center is halfway between the vertices (-3, 4) and (-3, 8). Apply the midpoint formula.

`\begin{gathered} (h,k)=((-3+-3)/(2),(4+8)/(2)) \\ =(-3,6) \end{gathered}`

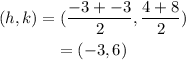
Next, find the square of a.

The length of the transverse axis is, 2a, bounded by the vertices. So, to find the square of a, determine the distance between the y-coordinates of the vertices.

`\begin{gathered} 2a=|4-8| \\ 2a=4 \\ a=(4)/(2)=2 \\ a^2=2^2=4 \end{gathered}`

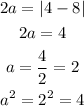
Find the square of c. The coordinates of the foci are (h, k+c) and (h, k-c). So (h, k- c) = (-3, 3) and (h, k+c) = (-3, 9). Use the y-coordinate from either of these points to solve for c. Using the point (-3, 3) and substituting k = 6.

`\begin{gathered} k+c=9 \\ 6+c=9 \\ c=9-6 \\ =3 \\ c^2=3^2=9 \end{gathered}`

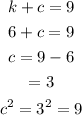
Solve for square of b using the equation

`b^2=c^2-a^2`

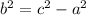
Substitute the obtained values.

`\begin{gathered} b^2=9-4 \\ =5 \end{gathered}`

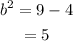
Finally, substitute the obtained values into the standard form of the equation

`\begin{gathered} ((y-6)^2)/(4)-((x-(-3))^2)/(9)=1 \\ ((y-6)^(2))/(4)-((x+3)^2)/(9)=1 \end{gathered}`

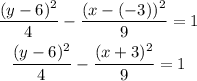
Final Answer: The equation of the required hyperbola is

`((y-6)^2)/(4)-((x+3)^2)/(9)=1`