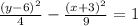Given:
Foci of the hyperbola = (-3,3), (-3, 9)
Vertices of the hyperbola = (-3, 4), (-3, 8)
Required: Equation of the hyperbola
Step-by-step explanation:
The x-coordinates of the vertices and foci are same, so the transverse axis is parallel to the y-axis. Thus, the equation of the hyperbola will have the form
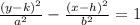
First, identify the center (h, k). The center is halfway between the vertices (-3, 4) and (-3, 8). Apply the midpoint formula.

Next, find the square of a.
The length of the transverse axis is, 2a, bounded by the vertices. So, to find the square of a, determine the distance between the y-coordinates of the vertices.
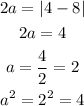
Find the square of c. The coordinates of the foci are (h, k+c) and (h, k-c). So (h, k- c) = (-3, 3) and (h, k+c) = (-3, 9). Use the y-coordinate from either of these points to solve for c. Using the point (-3, 3) and substituting k = 6.

Solve for square of b using the equation
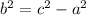
Substitute the obtained values.
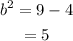
Finally, substitute the obtained values into the standard form of the equation
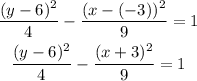
Final Answer: The equation of the required hyperbola is