We will use the following trigonometric laws, sine law and cosine law.
Cosine law is :
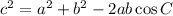
Sine law is :
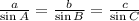
From the problem, we have B = 74 degrees, a = 38 and c = 41
We need first to find the value of b using cosine law, note that the missing value is b, so we will rewrite the cosine law as b in terms of a and c :
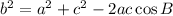
Substitute the given values and solve for b :
![\begin{gathered} b^2=38^2+41^2-2(38)(41)\cos 74 \\ b^2=3125-3116\cos 74 \\ b=\sqrt[]{3125-3116\cos 74} \\ b=47.60 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/17t87th562aahq83n6nz7vq9a0hnzmggad.png)
Next is to use the sine law with B = 74 degrees, b = 47.60 and a = 38.
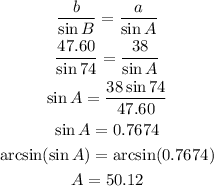
The answer is C. m∠A = 50.1 degrees