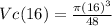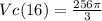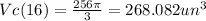Given the function
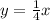
the vertical line is given by the point
( x , 0 )
the area of the triangle is
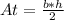
where
base= value of x
height=value of y
then
the expression of the area as a function of x is
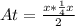
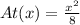
Then when x=5
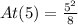
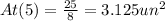
The volume of the cone is given by
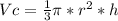
where
h= value of x
r= value of y
then the volume of the cone as a function of x is
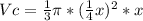
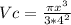
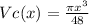
The volume of the cone when x=16 is