Answer:
The direction of the resultant force on the ball = 28.3°
Step-by-step explanation:
Sue's foot exerts a force of 28.85 N East
Jenny's foot exerts a force of 15.53 N North
This can be represented diagrammatically as:
The magnitude of the resultant force, R, is calculated using the Pythagora's theorem
![\begin{gathered} R^2=28.85^2+15.53^2 \\ R=\sqrt[]{28.85^2+15.53^2} \\ R=32.76N \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/xlnhcvj92b5dv9f73w7is2c17ps1641b3d.png)
The resultant force on the ball is 32.76N
The direction of the resultant force is given as:
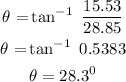
The direction of the resultant force on the ball = 28.3°