Question

According to a survey conducted at the local DMV, 55% of drivers who drive to work stated that they regularly exceed the posted speed limit on their way to work. Suppose that this result is true for the population of drivers who drive to work. A random sample of 15 drivers who drive to work is selected. Use the binomial probabilities table (Table I of Appendix B) or technology to find to 3 decimal places the probability that the number of drivers in this sample of 15 who regularly exceed the posted speed limit on their way to work is

Answer 1

`\begin{gathered} n=15 \\ p=(55)/(100)=0.55 \end{gathered}`

For a sample of 15 (n=15) you get the next P(X=x) in the binomial probabilities table:

As you have a p=0.55 (55%) Use the column of 0.55

a. At most 5

`P(X\le5)`

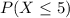
To find the probability that x ≤ 5:

-Identify in the table the probability when x=5, x=4, x=3, x=2, x=1 and x=0:

-Use the next formula to find P(x ≤ 5):

`\begin{gathered} P(X\le5)=P(X=0)+P(X=1)+P(X=2)+P(X=3)+P(X=4)+P(X=5) \\ \end{gathered}`
`\begin{gathered} P(X\le5)=0.000+0.000+0.001+0.006+0.025+0.077 \\ P(X\le5)=0.109 \end{gathered}`

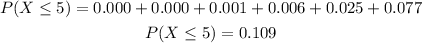
Answer a: Probability = 0.109

b. 6 to 9:

`P(6\le X\le9)_{}`

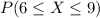
-Identify in the table the probability when x=6, x=7, x=8, x=9: