Question

Question 60. State wether the triangle is is an Isosceles triangle, a right triangle,neither or both.

Answer 1

(57) We want to find the length of each side of the triangle with sides

`P_1(2,1),P_2(-4,1),P_3(-4,-3)`

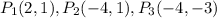
Using the distance formula we have

`d = √((x_2 - x_1)^2 + (y_2-y_1)^2)`

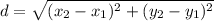
Between P1 and P2, we have

`\begin{gathered} d=√((-4-2)^2+(1-1)^2) \\ d=√((-6)^2) \\ P_1P_2=√(36)=6\text{ units } \end{gathered}`

Between P2 and P3, we have

`\begin{gathered} P_2P_3=√((x_2 - x_1)^2 + (y_2-y_1)^2) \\ P_2P_3=√(\left(-4-(-4)\right)^2+\left(-3-1\right)^2) \\ =√(0+(-4)^2) \\ =√(16)=4\text{ units } \end{gathered}`

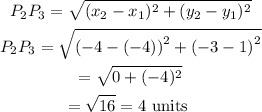
Between P1 and P3, we have

`\begin{gathered} P_1P_3=√(\left(-4-2\right)^2+\left(-3-1\right)^2) \\ =√((-6)^2+(-4)^2) \\ =√(36+16) \\ =√(52)\text{ units } \end{gathered}`

Now looking at sides P1P2 = 6 units and P2P3 = 4 units we can see that

`\begin{gathered} √(6^2+4^2) \\ =√(36+16) \\ √(52)=P_1P_3 \end{gathered}`

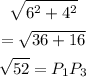
Hence, this is a right-angle triangle because it is in accordance with Pythagorean theorem. P1P3 is the hypotenuse