SOLUTION
(57) We want to find the length of each side of the triangle with sides
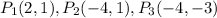
Using the distance formula we have
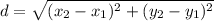
Between P1 and P2, we have
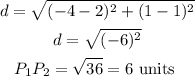
Between P2 and P3, we have
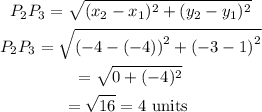
Between P1 and P3, we have
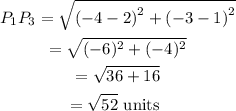
Now looking at sides P1P2 = 6 units and P2P3 = 4 units we can see that
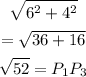
Hence, this is a right-angle triangle because it is in accordance with Pythagorean theorem. P1P3 is the hypotenuse