Question

Find the ratio of the area of triangles ABC to the area of triangle XYZ

Answer 1

The ratio of the area of triangles ABC to the area of triangle XYZ is 1/9

STEP - BY - STEP EXPLANATION

What to find?

The ratio of the area of triangles ABC to the area of triangle XYZ

To solve the given question, we will follow the steps below:

Step 1

Find the value of the base of triangle XYZ (length XY).

From the given figure, YW = WX

⇒YW = WX =15

⇒ XY = WX + YW = 15 + 15 = 30

Hence, the base = 30.

Step 2

Identify the value of the height of the triangle XYZ.

Height =36

Step 3

Recall the formula for calculating the area of a triangle.

Area = base x height

Step 4

Find the area of triangle XYZ.

Substitute the value of the base and height into the formula in step 3 and simplify.

That is;

Area = 30 x 36 =1080

Step 5

Determine the height of triangle ABC (length CD).

Using the trigonometric ratio;

sinθ = opposite / hypotenuse

Where opposite = h= height, hypotenuse = 13 and θ= 67 degree.

⇒sin67 = h/13

⇒ h = 13sin67

⇒h ≈ 12

Hence, height of traingle ABC = 12

Step 6

Find the base of triangle ABC.

Given that;

BD =AD = 5

⇒ BA = BD + AD = 5 + 5 = 10

Hence, base= 10

Step 7

Calculate the area of triangle ABC .

Using the formula;

Area = base x height

=10 x 12

= 120

Hence, area of triangle ABC = 120

Step 8

Proceed to find the ratio of area of ΔABC to the area of ΔXYZ.

`\text{Ratio}=\frac{area\text{ of }\Delta ABC}{\text{area of }\Delta XYZ}`
`=(120)/(1080)=(12)/(108)=(1)/(9)`

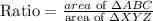
Therefore, the ratio of the area of triangles ABC to the area of triangle XYZ is 1/9