Given: The value of a and the vertex of the following parabola are given
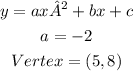
Required: To find the x-intercepts of the given parabola.
Explanation: The vertex of the parabola is at (5,8). The x coordinate of the vertex is given by

Hence, putting x=5 and a=-2 we get,
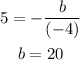
Now the y coordinate of the vertex is 8, and the value of c can be found by putting x=5 in the equation of the parabola.

Hence the equation of the parabola is
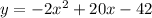
The x-intercepts can be determined by putting y=0 as follows
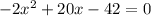
which gives,

Following is the graph
Final Answer: The parabola has 2 x-intercepts and the vertex lies above the x-axis.