Question

The value of a in y=ax²+bx+c and the vertex of the parabola are given. How many x-intercepts does the parabola have? Explain how you arrived at this number.a= -2; vertex at (5,8)The parabola has x-intercept(s), because the parabola opensand the vertex isthe x-axis.

Answer 1

Given: The value of a and the vertex of the following parabola are given

`\begin{gathered} y=ax²+bx+c \\ a=-2 \\ Vertex=(5,8) \end{gathered}`

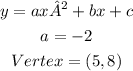
Required: To find the x-intercepts of the given parabola.

Explanation: The vertex of the parabola is at (5,8). The x coordinate of the vertex is given by

`x=-(b)/(2a)`

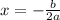
Hence, putting x=5 and a=-2 we get,

`\begin{gathered} 5=-(b)/((-4)) \\ b=20 \\ \end{gathered}`

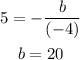
Now the y coordinate of the vertex is 8, and the value of c can be found by putting x=5 in the equation of the parabola.

`\begin{gathered} 8=-2(5)^2+20(5)+c \\ c=-42 \end{gathered}`

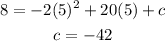
Hence the equation of the parabola is

`y=-2x^2+20x-42`

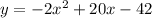
The x-intercepts can be determined by putting y=0 as follows

`-2x^2+20x-42=0`

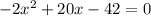
which gives,

`\begin{gathered} x^2-10x+21=0 \\ (x-7)(x-3)=0 \\ x=7\text{ and} \\ x=3 \end{gathered}`

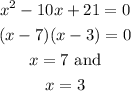
Following is the graph

Final Answer: The parabola has 2 x-intercepts and the vertex lies above the x-axis.