So we have a function defined by 5 ordered pairs:

This means that the function takes five different x values and associate each of them with a y value. The inverse function exchanges x values with y values so the pairs that define it are those of f but with their coordinates interchanged. Then the inverse function is:
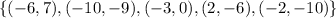
And that's the first answer.
Then we need to find the domain of the inverse function. This is given by all the x values for which there's an associated y value. In other terms, the domain is composed of all the x values of the points that define the function. Ordering them from lowest to highest we get the domain of the inverse:
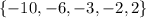
And that's the second answer.