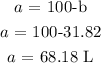Question

How much 16% acid solution and how much of a 60% acid solution should be mixed to make 100 liters of 30% acid solution?

Answer 1

68.18 L of 16% acid solution and 31.82 L of 60% acid solution

Step-by-step explanation:

Let the number of liters of 16% acid solution be a

Let the number of liters of 60% acid solution be b

The sum of both will give the 100

Mahematically, we can write this as follows;

`a\text{ + b = 100}`

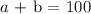
Secondly, if we multiply each concentration by the number of liters and sum it up, it will be equal to the total concentration multiplied by its number of liters

Kindly note that 16% = 16/100 = 0.16

60% = 60/100 = 0.6

30% = 30/100 = 0.3

Thus, we have it that:

`\begin{gathered} 0.16a\text{ + 0.6b = 100(0.3)} \\ 0.16a\text{ + 0.6b = 30} \end{gathered}`

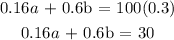
Now, we have two equations to solve simultaneously

From equation 1:

`a\text{ = 100-b}`

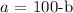
Substitute this into equation ii

`\begin{gathered} 0.16(100-b)\text{ + 0.6b = 30} \\ 16-0.16b\text{ + 0.6b = 30} \\ 0.6b-0.16b\text{ = 30-16} \\ 0.44b\text{ = 14} \\ b\text{ = }(14)/(0.44) \\ b\text{ = 31.82 L} \end{gathered}`

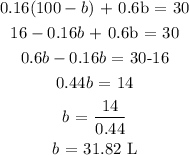
Finally, we can get a from susbtituting the value of b into the first equation

Mathematically, we have this as:

`\begin{gathered} a\text{ = 100-b} \\ a\text{ = 100-31.82} \\ a\text{ = 68.18 L} \end{gathered}`