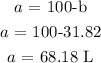Answer:
68.18 L of 16% acid solution and 31.82 L of 60% acid solution
Step-by-step explanation:
Let the number of liters of 16% acid solution be a
Let the number of liters of 60% acid solution be b
The sum of both will give the 100
Mahematically, we can write this as follows;
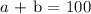
Secondly, if we multiply each concentration by the number of liters and sum it up, it will be equal to the total concentration multiplied by its number of liters
Kindly note that 16% = 16/100 = 0.16
60% = 60/100 = 0.6
30% = 30/100 = 0.3
Thus, we have it that:

Now, we have two equations to solve simultaneously
From equation 1:
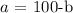
Substitute this into equation ii
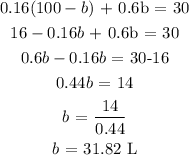
Finally, we can get a from susbtituting the value of b into the first equation
Mathematically, we have this as: