Question

the shorter leg of a right triangle is 7 m shorter than the longer leg. the hypotenuse is 7 m longer than the longer leg. find the side lengths of the triangle. length of the shorter leg:length of the longer leg:length of the hypotenuse:

Answer 1

Step-by-step explanation:

Let the length of the longer leg = x m

The shorter leg of a right triangle is 7m shorter than the longer leg. therefore:

Length of the shorter leg = (x-7) m

The hypotenuse is 7m longer than the longer leg.

Length of the hypotenuse = (x+7) m

We solve for x using Pythagoras Theorem.

`\text{Hypotenuse}^2=\text{Opposite}^2+\text{Adjacent}^2^{}`

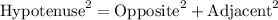
This gives us:

`\begin{gathered} (x+7)^2=x^2+(x-7)^2 \\ (x+7)(x+7)=x^2+(x-7)(x-7) \\ x^2+14x+49=x^2+x^2-14x+49 \\ 2x^2-x^2-14x-14x-49+49=0 \\ x^2-28x=0 \\ x(x-28)=0 \\ x-28=0\text{ or x=0} \\ x=28\text{ meters} \end{gathered}`

Therefore:

• Length of the shorter leg: 28-7 = 21 meters

,

• Length of the longer leg: 28 meters

,

• Length of the hypotenuse: ​28+7 = 35 meters