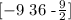Question

Can anyone answer this? i’ve had a hard time answering it. It’s a practice problem that I just need answered

Answer 1

To get the value of m x H

We will first get the value of m and then H

To get the value of m

`3\begin{pmatrix}-1 & 2 \\ 4 & 8\end{pmatrix}=(2)/(3)m\begin{pmatrix}-1 & 2 \\ 4 & 8\end{pmatrix}`

`\begin{gathered} \mathrm{Switch\: sides} \\ \\ (2)/(3)m\begin{pmatrix}-1 & 2 \\ 4 & 8\end{pmatrix}=3\begin{pmatrix}-1 & 2 \\ 4 & 8\end{pmatrix} \end{gathered}`

`(2)/(3)m\begin{pmatrix}-1 & 2 \\ 4 & 8\end{pmatrix}=\begin{pmatrix}-3 & 6 \\ 12 & 24\end{pmatrix}`

`\begin{gathered} (2)/(3)m\begin{pmatrix}-1 & 2 \\ 4 & 8\end{pmatrix}=\begin{pmatrix}-3 & 6 \\ 12 & 24\end{pmatrix} \\ \\ \mathrm{Multiply\: both\: sides\: by\: }(3)/(2) \\ \\ (3)/(2)\cdot(2)/(3)m\begin{pmatrix}-1 & 2 \\ 4 & 8\end{pmatrix}=(3)/(2)\begin{pmatrix}-3 & 6 \\ 12 & 24\end{pmatrix} \\ \\ m\begin{pmatrix}-1 & 2 \\ 4 & 8\end{pmatrix}=(3)/(2)\begin{pmatrix}-3 & 6 \\ 12 & 24\end{pmatrix} \end{gathered}`

`\begin{gathered} m\begin{pmatrix}-1 & 2 \\ 4 & 8\end{pmatrix}=\begin{pmatrix}-(9)/(2) & 9 \\ 18 & 36\end{pmatrix} \\ \mathrm{Multiply\: both\: sides\: of\: the\: equation\: by}\: \begin{pmatrix}-1 & 2 \\ 4 & 8\end{pmatrix}^(-1)\: \mathrm{from\: the\: right} \\ XA=B\quad \Rightarrow\quad \: X=BA^(-1) \\ m=\begin{pmatrix}-(9)/(2) & 9 \\ 18 & 36\end{pmatrix}\begin{pmatrix}-1 & 2 \\ 4 & 8\end{pmatrix}^(-1) \end{gathered}`

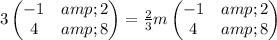
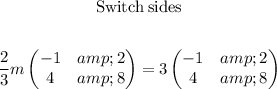
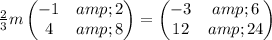
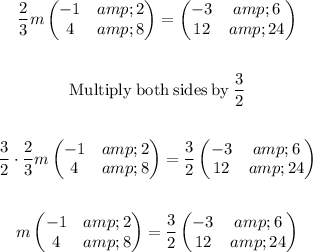
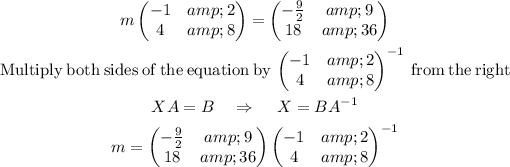
The next is to get H

`(H\text{ +\lbrack{}1 4 -2\rbrack) + \lbrack{}3 2 -6\rbrack = \lbrack-2 8 -1\rbrack + (\lbrack{}1 4 -2\rbrack + \lbrack{}3 2 -6\rbrack)}`

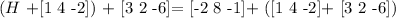
Let H be represented by [ A B C] so that

`\mleft(\begin{pmatrix}A & B & C\end{pmatrix}+\begin{pmatrix}1 & 4 & -2\end{pmatrix}\mright)+\begin{pmatrix}3 & 2 & -6\end{pmatrix}=\mleft(\begin{pmatrix}-2 & 8 & -1\end{pmatrix}\mright)+\mleft(\begin{pmatrix}1 & 4 & -2\end{pmatrix}+\begin{pmatrix}3 & 2 & -6\end{pmatrix}\mright)`

=>

`\mleft(\begin{pmatrix}A & B & C\end{pmatrix}+\begin{pmatrix}1 & 4 & -2\end{pmatrix}\mright)+\begin{pmatrix}3 & 2 & -6\end{pmatrix}=\mleft(\begin{pmatrix}-2 & 8 & -1\end{pmatrix}\mright)+\mleft(\begin{pmatrix}1 & 4 & -2\end{pmatrix}+\begin{pmatrix}3 & 2 & -6\end{pmatrix}\mright)`

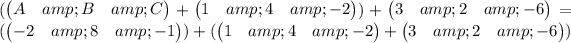
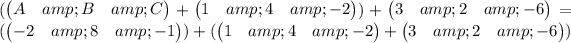
=> Simplifying further

`\begin{pmatrix}A+4 & B+6 & C-8\end{pmatrix}=\begin{pmatrix}2 & 14 & -9\end{pmatrix}`

`A=-2,\: C=-1,\: B=8`

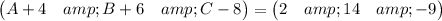
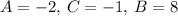
Thus,

`\begin{gathered} H=\lbrack A\text{ B C\rbrack} \\ H=\lbrack-2\text{ }8\text{ -1\rbrack} \end{gathered}`

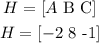
The final step will be to find m x H

To simplify m

Therefore

`m=(9)/(2)`

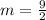
Therefore

m x H will be

`(9)/(2)*\lbrack-2\text{ 8 -1\rbrack}`

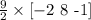
The answer is:

`\lbrack-9\text{ 36 -}(9)/(2)\rbrack`