Question

The first two terms of an arithmetic sequence are 7 and 4. Find the 7th term.

Answer 1

EXPLANATION

If the first two terms of an arithmetic sequence are 7 and 4, then we know that an arithmetic sequence has a constant difference d and is defined by

`a_n=a_1+(n+1)d`

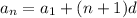
Check wheter the difference is constant:

Compute the differences of all the adjacent terms:

`d=a_(n+1)-a_n`

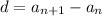
Replacing terms:

4-7 = -3

The difference between all of the adjacent terms is the same and equal to

d = -3

The first element of the sequence is

`a_1=7`
`a_n=a_1+(n+1)d`

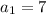
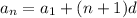
Therefore, the nth term is computed by

d= -3

`a_n=7+\text{ (n-1)}\cdot(-3)`

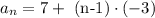
Refine

d= -3 ,

`a_n=-3n+10`

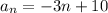
Now, replacing n=7

`a_7=-3\cdot7+10\text{ = -11}`

So, the answer is -11.