EXPLANATION
If the first two terms of an arithmetic sequence are 7 and 4, then we know that an arithmetic sequence has a constant difference d and is defined by
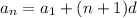
Check wheter the difference is constant:
Compute the differences of all the adjacent terms:
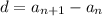
Replacing terms:
4-7 = -3
The difference between all of the adjacent terms is the same and equal to
d = -3
The first element of the sequence is
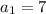
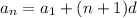
Therefore, the nth term is computed by
d= -3
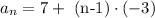
Refine
d= -3 ,
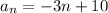
Now, replacing n=7
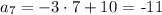
So, the answer is -11.