The expression we have is:

First, we use the following property of natural logarithms:
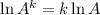
the exponent is lowered.
We apply this to our expression:
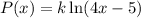
Next, we use the given condition:
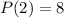
What this means is that when x=2, the value of P(x) is 8.
We need to substitute this two values into our expression:

We solve the expression inside the natural logarithm:
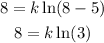
Now, since ln(3)=1.1 we get:

We solve for k by dividing both sides by 1.1:
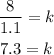
The value of k is 7.3