The population growth formula is :

where P = total population after time t
Po = initial population
e = euler's number
r = percent rate of growth
t = time in years
From the problem, the population doubles in 15 years, so we have :
P = 2Po
t = 15
Using the formula above :
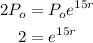
Take ln of both sides :
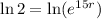
Note that :
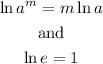
The natural logarithm of a raised to m is the same as m multiplied by the natural logarithm of a.
So the equation will be :
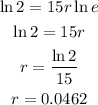
The answer is 0.0462 or 4.62%