Question

What are the coordinates ofpoint P on the directed linesegment from A (-5, -4) toB (5, 1) that partitions thesegment into a ratio of 3 to 2?(1 point)(0, -3)(1, -1)(11,4)(-1, -2)

Answer 1

We have to find the coordinates of point P.

It is located in the segment AB and it is located such as the ratio AP:PB is 3:2.

We can think of the ratio as if the segment has 3+2=5 equally sized subsegments, where 3 subsegments are the distance from A to P and 2 subsegments are the distance from P to B:

As we have A and B located in certain coordinates of xy-plane, we can use the fact that P is goin to be 3/5 of the distance between AB in the x-coordinates and also in the y-coordinates, so we can calculate each coordinate separately:

`x_p=x_a+(3)/(5)(x_b-x_a)=-5+(3)/(5)(5-(-5))=-5+(3)/(5)\cdot10=-5+6=1`
`y_p=y_a+(3)/(5)(y_b-y_a)=-4+(3)/(5)(1-(-4))=-4+(3)/(5)\cdot5=-4+3=-1`

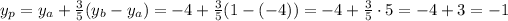
The coordinates of P are