Question

Clark's Country Pet Resort is fencing a new play area for dogs. The manager has purchased 260yd of fence to enclose a rectangular pen. The area of the pen must be 3784yd^2. What are the dimensions of the pen?The length(longer side) is __ yd.The width(shorter side) is __yd.

Answer 1

The manager purchased 260 yd of fence for the pen, this tells us that the perimeter of the pen is 260 yd.

Step 1. Let's call the length of the pen "l" and the width of the pen "w".

Since the pen is rectangular, the formula to calculate the perimeter is:

`2l+2w`

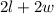
And since we already know the value of the perimeter, we have the following equation:

`2l+2w=260`

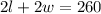
Step 2. We can also find an expression for the area of the pen.

The formula for the area of a rectangle is:

`l* w`

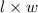
And since in this case, the area of the pen is 3784 yd^2:

`l* w=3784`

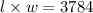
Step 3. So far we have two equations:

`\begin{gathered} 2l+2w=260 \\ l* w=3784 \end{gathered}`

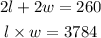
Step 4. The next step is to solve for l in the first equation:

`\begin{gathered} 2l+2w=260 \\ 2l=260-2w \\ l=130-w \end{gathered}`

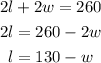
And substitute that into the second equation:

`\begin{gathered} l* w=3784 \\ (130-w)* w=3784 \end{gathered}`

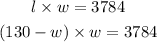
We have found an equation that only depends on w.

Step 5. Apply the distributive property on the previous equation:

`130w-w^2=3784`

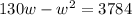
Step 6. Re-arrange the equation so that is equal to 0:

`-w^2+130w-3784=0`

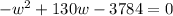
We have a quadratic equation that we will solve using the general quadratic formula.

First, we define our variables a, b and c as the coefficients of w^2, w, and the independent term:

`\begin{gathered} a=-1 \\ b=130 \\ c=-3784 \end{gathered}`

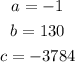
Step 7. The general quadratic formula is:

`w=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Substituting a, b, and c:

`w=\frac{-130\pm\sqrt[]{(130)^2-4(-1)(-3784)}}{2(-1)}`

And we start solving what is inside the square root:

`w=\frac{-130\pm\sqrt[]{16900-15136}}{-2}`

Solving the subtraction:

`\begin{gathered} w=\frac{-130\pm\sqrt[]{1764}}{-2} \\ \end{gathered}`

Solving the square root:

`w=(-130\pm42)/(-2)`

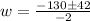
And there will be two solutions for w, one using the + sign and the other using the - sign.

First, using the - sign we get:

`w=(-130-42)/(-2)=(-172)/(-2)=86`

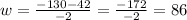
And the using the + sign:

`\begin{gathered} w=(-130+42)/(-2) \\ w=(-88)/(-2) \\ w=44 \end{gathered}`

We have two answers for w, but we keep the smaller because the width is the shorter side.

`w=44`

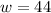
The width is 44 yd.

Step 7. Now we substitute this value of w into the equation from step 1:

`\begin{gathered} 2l+2w=260 \\ 2l+2(44)=260 \\ \text{And solve for l:} \\ 2l+88=260 \\ 2l=260-88 \\ 2l=172 \\ l=(172)/(2) \\ l=86 \end{gathered}`

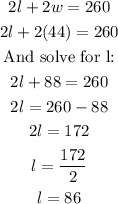
The length is 86 yd.

Answer:

length: 86 yd

width: 44yd