Question

Can you please have this solve? I am Reviewing for a final thank you

Answer 1

Part A. We are given that the deformation of a string from its equilibrium position is given by the following equation:

`r=2\cos\theta+√(3)`

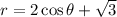
To determine the value of the angle for which the spring in at equilibrium we need to set the equation to zero:

`2\cos\theta+√(3)=0`

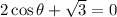
Now, we solve for the time. First, we subtract the square root of 3 to both sides:

`2\cos\theta=-√(3)`

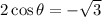
Now, we divide both sides by 2:

`\cos\theta=(-√(3))/(2)`

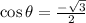
now, we take the inverse function of the cosine:

`\theta=cos^(-1)((-√(3))/(2))`

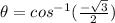
Solving the operation:

`\theta=(5\pi)/(6),(7\pi)/(6)`

This two angles apply for the interval of time:

`(0,2\pi)`

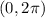
Part B. Now, we are asked to double the angle. We get the following equation:

`r=2\cos(2\theta)+√(3)`

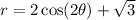
Now, we set the equation to zero:

`2\cos(2\theta)+√(3)=0`

Now, we solve for the time similarly as we did in the previous point:

`2\theta=cos^(-1)((-√(3))/(2))`

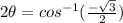
Now, we solve the right side:

`2\theta=(5\pi)/(6),(7\pi)/(6)`

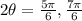
Dividing both sides by 2:

`\theta=(5\pi)/(12),(7\pi)/(12)`

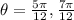
In this case, for the interval between 0 and 2 pi we have that the possibe values of time are:

`\theta=(5\pi)/(12),(7\pi)/(12),(19\pi)/(12),(17\pi)/(12)`

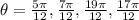
The difference with the values in part A is that the spring now passes through the equolibrium point at a greater frequency.

Part C. We are given that another spring has the following equation :

`g(\theta)=1-sin^2\theta+√(3)`

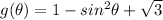
To determine the value of time where the spring are at equilibrium we set both equations equal:

`2\cos\theta+√(3)=1-sin^2\theta+√(3)`

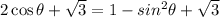
We can cancel out the square root of 3:

`2\cos(\theta)=1-s\imaginaryI n^2\theta`

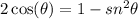
Now, we use the following trigonometric identity:

`\cos^2\theta=1-\sin^2\theta`

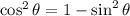
Substituting we get:

`2\cos\theta=\cos^2\theta`

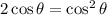
Now, we subtract the left side:

`\cos^2\theta-2\cos\theta=0`

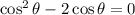
Now, we take cosine as common factor:

`\cos\theta(\cos\theta-2)=0`

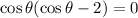
Now, we set each factor to zero:

`\begin{gathered} cos\theta=0 \\ \theta=n\pi-(\pi)/(2) \end{gathered}`

For:

`n=1,2,3,4...`

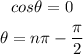
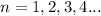
For the second factor we have:

`\begin{gathered} cos\theta-2=0 \\ \cos\theta=2 \\ No\text{ solutions} \end{gathered}`

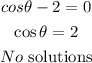
Therefore, the times are the solution to the first factor.