Answer:
Height: 30.25 feet.
Step-by-step explanation:
The equation of the ball's path is given as:
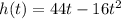
To find the maximum point, first, find the derivative of the function:
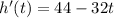
Next, set the derivative equal to 0 and solve for t:
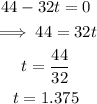
The maximum height occurs when the time, t=1.375 seconds.
Next, substitute it into h(t):
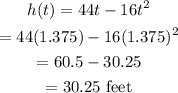
The maximum height, h(t) that the ball will reach is 30.25 feet.