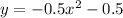The Solution:
Given the equation of the parabola in vertex form:
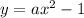
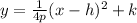
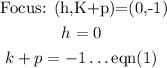
By directrix:
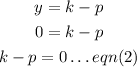
Solving eqn(1) and eqn(2) simultaneously, we get
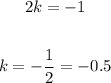
So, the directrix is:
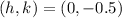
So, the equation of the parabola is
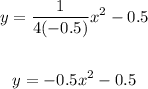
So, the value of p is -0.5
Thus, the equation of the parabola in vertex form is: