Given
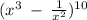
We are asked to find the number of terms the expression would have when expanded. This can be seen below.
Step-by-step explanation
To find the number of terms in the expression, we can apply the pascal triangle easily.
The values above represent the coefficient of the terms of each expansion when the exponential of the expression is 1 up until 7.
Notice that if the exponent is one we have two coefficients and therefore two terms. If the exponent is two, the number of coefficients is three and therefore we have three terms.
Hence, we can extrapolate and say that if the exponential is 10, the number of coefficients will be 11 and the number of terms will therefore be 11.
Answer: Option C