From the information given in the statement we know that:
• Triangle truck rentals charge ,$35 per day and 35 cents a, mile,.
,
• Circle rent a truck charge ,$60 a day and 30 cents a ,mile,.
On the other hand, let be x the number of miles he would need to drive in one day. So, we can write the following equation:
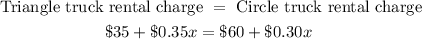
Now, we can solve the equation for x
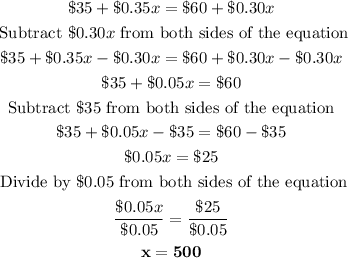
Therefore, he would need to drive 500 thousand in one day for both companies to have the same total cost