Answer: Option A
We are given a table in the question which provided us with the information of number of laps and time
Let x = number of laps
y = time
Firstly, we will pick any two points on the table
Let x1 = 4, x2 = 20, y1 = 96, and y2 = 340
![\begin{gathered} \text{The slope-intercept form of equation is written as} \\ y\text{ = mx + b, where m = slope and b = intercept} \\ \text{Slope = }\frac{y2\text{ - y1}}{x2\text{ - x1}} \\ \text{Slope = }\frac{340\text{ - 96}}{20\text{ - 4}} \\ \text{Slope = }(244)/(16) \\ \text{Slope = 15.25} \\ \text{Slope = 15.3} \\ \text{The equation for a given point} \\ (y\text{ - y1) = m(x -x1)} \\ (y\text{ - 96) = 15.3(x - 4)} \\ \text{Open the parentheses} \\ y\text{ - 96 = 15.3x - 61.2} \\ y\text{ = 15.3x - 61.2 +96} \\ y\text{ = 15.3x +10.4 } \end{gathered}]()
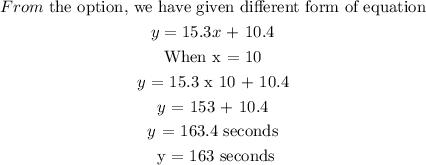
Option A is the only option that satisfy the condition