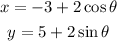Answer:
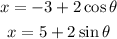
Explanations
Given the parametric equations represented by (x + 3)^2 + (y − 5)^2 = 4.
We need to determine the parametric equation that represents the equation. Checking the first parametric equation
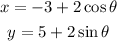
Substitute the parametric equation into the left-hand side of the parametric equation as shown:

Recall from trigonometry identity that:
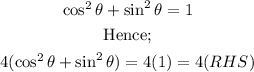
Since the result gave the right-hand side of the equation on simplification hence the correct sets of parameters equation are: