We can use the distance formula to easily find the speed of the plane in still air.
Let it be "x".
With Tailwind, the airplane goes faster and against the Tailwing, it goes slower.
We know,
D = RT
Where
D is distance
R is rate
T is time
Thus,
For the first leg, we can write:
R = x + 25
T = 5 hours
So,
D = (x+25)(5)
For the second leg, we can write:
R x - 25
T = 5.5 hours
So,
D = (x - 25)(5.5)
Both the distances are same, thus, we can equate them and do algebra to solve for x. The steps are shown below:
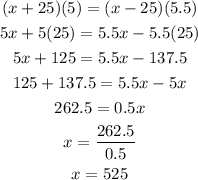
Thus,
The speed of the airplane in still air is
525 mph