Question

an airplane flew for 5 hours with a Tailwind of 25 kilometers per hour . the return flight against the same wind took 5.5 hours . find the speed of the airplane in still air.

Answer 1

We can use the distance formula to easily find the speed of the plane in still air.

Let it be "x".

With Tailwind, the airplane goes faster and against the Tailwing, it goes slower.

We know,

D = RT

Where

D is distance

R is rate

T is time

Thus,

For the first leg, we can write:

R = x + 25

T = 5 hours

So,

D = (x+25)(5)

For the second leg, we can write:

R x - 25

T = 5.5 hours

So,

D = (x - 25)(5.5)

Both the distances are same, thus, we can equate them and do algebra to solve for x. The steps are shown below:

`\begin{gathered} \mleft(x+25\mright)\mleft(5\mright)=(x-25)(5.5) \\ 5x+5(25)=5.5x-5.5(25) \\ 5x+125=5.5x-137.5 \\ 125+137.5=5.5x-5x \\ 262.5=0.5x \\ x=(262.5)/(0.5) \\ x=525 \end{gathered}`

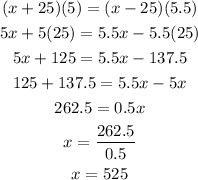
Thus,

The speed of the airplane in still air is

525 mph