Question

The vertices of quadrilateral JKLM are J(0,6), K(2,8), L(6,8), and M(6,4). Find the vertices of the image after a dilation with a scale factor of 1/2 centered at the origin and a reflection over the x-axis.

Answer 1

J' (0, -3)

K' (1, -4)

L' (3, -4)

M' (3, -2)

Step-by-step explanation

The quadilateral JKLM is transformed by dilating it with scale factor of 1/2 and then reflected over the x axis.

First, we dilate the quadilateral by 1/2 by multiplying each of the vertices by 1/2.

That is:

`\begin{gathered} J\Rightarrow\text{ }(1)/(2)(0,\text{ 6) = (0, 3)} \\ K\Rightarrow(1)/(2)(2,\text{ 8) = (1, 4)} \\ L\Rightarrow\text{ }(1)/(2)(6,\text{ 8) = (3, 4)} \\ M\Rightarrow\text{ }(1)/(2)(6,\text{ 4) = (3, 2)} \end{gathered}`

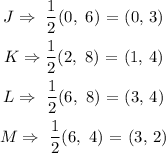
Now, we reflect it over the x axis. In doing this, the x cordinates remain the same but the y axis become the opposite.

That is:

J (0, 3) => J' (0, -3)

K (1, 4) => K' (1, -4)

L (3, 4) => L' (3, -4)

M (3, 2) => M' (3, -2)

Therefore, the vertices of the image are:

J' (0, -3)

K' (1, -4)

L' (3, -4)

M' (3, -2)